提起统计学,大家耳熟能详的一个论断是,统计学只能探讨相关关系而不能发现因果关系。一定程度上,这样说是有道理的。至于相关关系和因果关系有什么区别,这种区别对于统计推断来说又意味着什么,可能除了专业的做Causal Inference这部分的人以外,都没有什么概念。我们从Simpson悖论开始,希望能够说明相关性和因果性的区别和联系。这篇文章主要参考的是丁鹏老师在北大的讲义。
Yule-Simpson Paradox
2000年Pearl构造了一个在整个人群中吃药和康复的关系的例子。可以看到在整个人群中康复率与吃药与否是正相关的,但是当我们把人群细分成男性和女性群体的时候,会发现吃药与否其实和是否得病是负相关的。
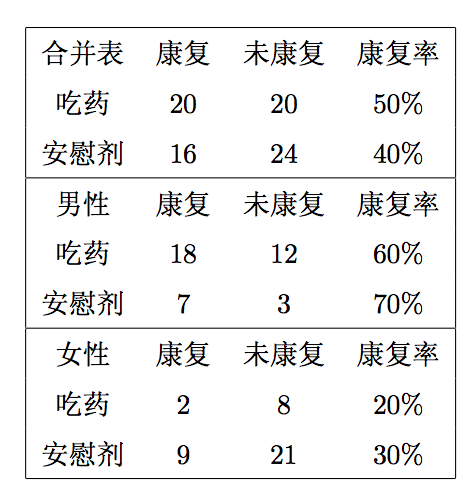
为什么会发生这种现象?我们用R简单生成一组随机数来看
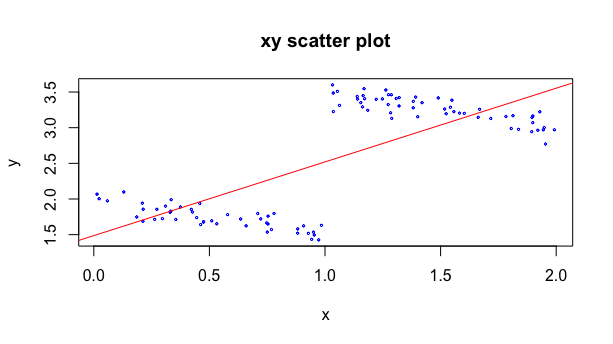
在这样一个随机数实例中,\(x\) 是0到2的均匀分布随机变量,而\(y\)和\(x\)的关系,在这个人工的例子中是线性的,可以表示为 \[ Y=-0.5X+2Z+2 \] 其中\(Z\) 是哑变量。在这个人工的实例中Z只表示\(X\)大于1还是小于等于1。很显然Y和Z也是相关的,并且相关关系比\(Y\)与\(X\)的关系要更大。但是可以如果我们对所有数据进行线性回归,可以看到结果是图中的这条红线。这表明如果我们不知道变量\(Z\)的存在而直接用变量\(X\)来解释变量\(Y\),会得到\(Y\)和\(X\)是正相关的这样错误的结论。这就是Simpson悖论
这个悖论的正式表述为:\(X\)和\(Y\)边缘上正相关,但是给定另外一个变量\(Z\)后,在\(Z\)的每一个水平上,\(X\)和\(Y\)可能负相关。正是因为这个悖论的存在,因果推断才会是一个如此困难的问题。
除了生造的数据之外,很多实际数据中也有类似的现象。流行病学中著名的健康工人效应:铀矿的工人虽然接触到放射性物质较多,但是其平均寿命不比常人短。这似乎说明铀矿对健康没有影响。但其实这里忽略的因素是,铀矿的工人通常身强力壮,不在铀矿工作的话寿命更长。在流行病学中,很多都会提到“混杂偏倚”其实就是Simpson悖论的实际表现。例如Rothman 2008.
在统计学中进行因果推断非常依赖于随机化实验。但是实际上我们得到的数据却往往是观测性的数据。因此一般即使得到了吸烟与肺癌的正相关,也不能断言吸烟导致肺癌,这是因为可能存在的某些没有观测到的因素,它既影响是否吸烟,也影响患病。例如某些基因可能使得人更容易吸烟,同时更容易得肺癌;存在这样的基因的人不吸烟也同样得肺癌。此时吸烟和肺癌之间是相关的但没有因果作用。