我们考虑残差独立同分布于某个密度函数\(f(\cdot)\)的线性回归模型： \[\begin{equation} Y_i=\mathbf{x}_i'\mathbf{\beta}+\varepsilon_i,\quad \varepsilon_i \ iid \sim f(\cdot) \label{model} \end{equation} \]
其中\(\mathbf{x}_i\)是第\(i\)条记录，它包含了\(p\)个变量,\(\beta\)中包含了截距项的存在. 在使用普通的最小二乘法进行线性回归建模时，我们经常假设\(f\)是正态分布的密度函数. 但是这个假设在实际数据中经常是不能满足的. 例如，如果真实的残差项是厚尾分布的，LSE的结果就会有巨大的偏差. 此时我们就要寻求更加稳健的方法来估计线性回归模型中的参数. 稳健回归的主要思路是降低具有较大残差的项在最小化过程中的权重，从而降低他们对于回归的影响. 在此基础上，产生了一系列的稳健回归方法. 本文主要讨论了M估计，中位数回归等方法，并给出了若干应用的例子. 主要参考线性回归的课本 Applied Regression Analysis 作者是 Norman R. Draper 和 Harry Smith. 第25章。
M估计
M估计量是稳健回归的一个一般性方法. 这类估计量主要是通过极大似然的类型得到的结论. 那么我们对模型中的系数参数\(\beta\)考虑极大似然估计 \[ \begin{equation} \widehat{\beta}=\arg\max_{\beta} \prod_{i=1}^nf(Y_i-\mathbf{x}_i'\beta) \end{equation} \] 或者等价的，最大化对数似然，得到 \[ \begin{equation} \widehat{\beta}=\arg\max_{\beta} \sum_{i=1}^n \log f(Y_i-\mathbf{x}_i'\beta) \end{equation} \] 即可得到一个估计量. 简单地应用这一思想，有简单的例子如：
- 当残差\(\varepsilon\)独立同正态分布时，极大似然估计即可导出OLS最小二乘估计: \[ \begin{equation} \beta = \arg \min_{\beta}\sum_{i=1}^n(\varepsilon_i)^2=\arg \min_{\beta}\sum_{i=1}^n\left(Y_i-\mathbf{x}_i\beta\right)^2 \label{OLS} \end{equation} \]
- 当残差\(\varepsilon\)独立同分布于双指数分布时，即 \[\begin{equation} f(\varepsilon)=\frac{1}{2\sigma}\exp\{-\frac{|\varepsilon|}{\sigma}\}, \quad (-\infty\leq \varepsilon\leq +\infty) \end{equation}\] 极大似然估计可以导出L1范数估计，即 \[\begin{equation} \beta = \arg \min_{\beta}\sum_{i=1}^n|\varepsilon_i|=\arg \min_{\beta}\sum_{i=1}^n|Y_i-\mathbf{x}_i\beta| \label{l1} \end{equation}\]
稍微推广上述想法，令\(\rho(u)\)是\(u\)的一个函数，假设\(s\)是对尺度的估计，我们定义一个稳健估计量，它能够最小化 \[ \begin{equation} \sum_{i=1}^n\rho\left(\frac{\varepsilon_i}{s}\right)=\sum_{i=1}^n\rho\left\{\frac{\mathbf{Y}_i-\mathbf{X}_i'\beta}{s}\right\} \label{M} \end{equation} \] 容易看出OLS和L1分别是\(\rho(u)=u^2,|u|\)时的特殊情形. 因此如果我们有残差具体分布的信息，我们将很容易构造出一个稳健估计量.但在实际问题中，我们往往不知道具体的残差分布的样子，因此我们常用的方法是通过选取一些特定形状的\(\rho(u)\)代入求解再进行选择.
当我们选定了\(\rho(u)\)的形式后，我们要求解回归方程.为此，我们令\(\Psi(u)=\partial \rho/\partial u\)，\(x_{ij}\)是\(x_i\)的第\(j\)个变量的值.因此对每个系数求导，得到\(p+1\)个方程，形如 \[ \begin{equation} \sum_{i=1}^n x_{ij}\Psi\left\{\frac{Y_i-\mathbf{x}_i'\beta}{s} \right\} = 0 \label{dereq} \end{equation} \] 利用Beaton and Turkey（1974,p.151)的迭代法数值求解. 定义权重 \[ \begin{equation} w_{i\beta}=\frac{\Psi\{(Y_i-\mathbf{x}_i'\beta)/s\}}{(Y_i-\mathbf{x}_i'\beta)/s} \label{weigts} \end{equation} \] 若分母为零则设该权重为1.可以利用矩阵写法表达成矩阵形式 \[ \begin{equation} \mathbf{X}'\mathbf{W}_{\beta}\mathbf{X}\mathbf{\beta}=\mathbf{X}'\mathbf{W}_{\beta}\mathbf{Y} \end{equation} \] 其中\(\mathbf{W}_{\beta}=\textit{diagonal}\{w_{1\beta},w_{2\beta},\cdots,w_{n\beta}\}\).这个方程和加权最小二乘法的解的方程具有相同的形式，因此也可以利用相同的迭代公式进行迭代求解.
在使用M估计时，还有一个重要的统计量是尺度因子\(s\)，在经验上我们对该参数有一个推荐的估计量 \[ \begin{equation} s = \text{median}|\varepsilon_i-\text{median}(\varepsilon_i)|/0.6745 \label{sest} \end{equation} \]
其他稳健回归方法
本章还介绍了其它稳健回归的方法，在这里列举如下
- 最小中值平方法：这种方法考虑的是在模型中最小化残差平方的中位数，即求 \[ \begin{equation} \beta = \arg\min_{\beta}\text{Median}(Y_i-\mathbf{x}_i'\beta)^2 \end{equation} \] 这种估计方法对计算复杂性的要求较高.
- 残差秩回归：这种方法的实质是最小化残差的加权和.假设\(a(\cdot)\)是一个加权函数，\(\mathbf{x}_i'\)是一条记录，则\(Y_i-\mathbf{x}_i'\beta\)是偏误. 考虑 \[ \begin{equation} D(\beta)=\sum_{i=1}^na\{R(Y_i-\mathbf{x}_i'\beta)\}\{Y_i-\mathbf{x}_i'\beta\}, \label{devia} \end{equation} \] 其中\(R\)是秩统计量. 这里的加权函数的一个常用选择是Wilcoxon的得分函数 \[ \begin{equation} a(i)=12^{1/2}\left\{\frac{i}{n+1}-\frac{1}{2}\right\} \end{equation} \] 在残差从小到大排序后，我们考虑 \[ \begin{equation} D_w(\beta)=12^{1/2}\left\{\frac{i}{n+1}-\frac{1}{2}\right\}\{Y_i-\mathbf{x}_i'\beta\} \end{equation} \] 调整这里的权重函数可以得到其它不同的秩回归方法.
- 其它的稳健回归方法还包括将最小二乘法求和中的每一项都替换成一个得分函数，例如秩. 目前这些方法还没有能够得到广泛的应用.
简单应用
我们介绍一个在Rousseeuw and Leroy (1987)中的电话数据集，自变量\(X\)是年份，因变量\(Y\)是比利时该年的电话通话次数.我们在该数据集上分别进行普通最小二乘回归，M估计和最小截断估计.结果为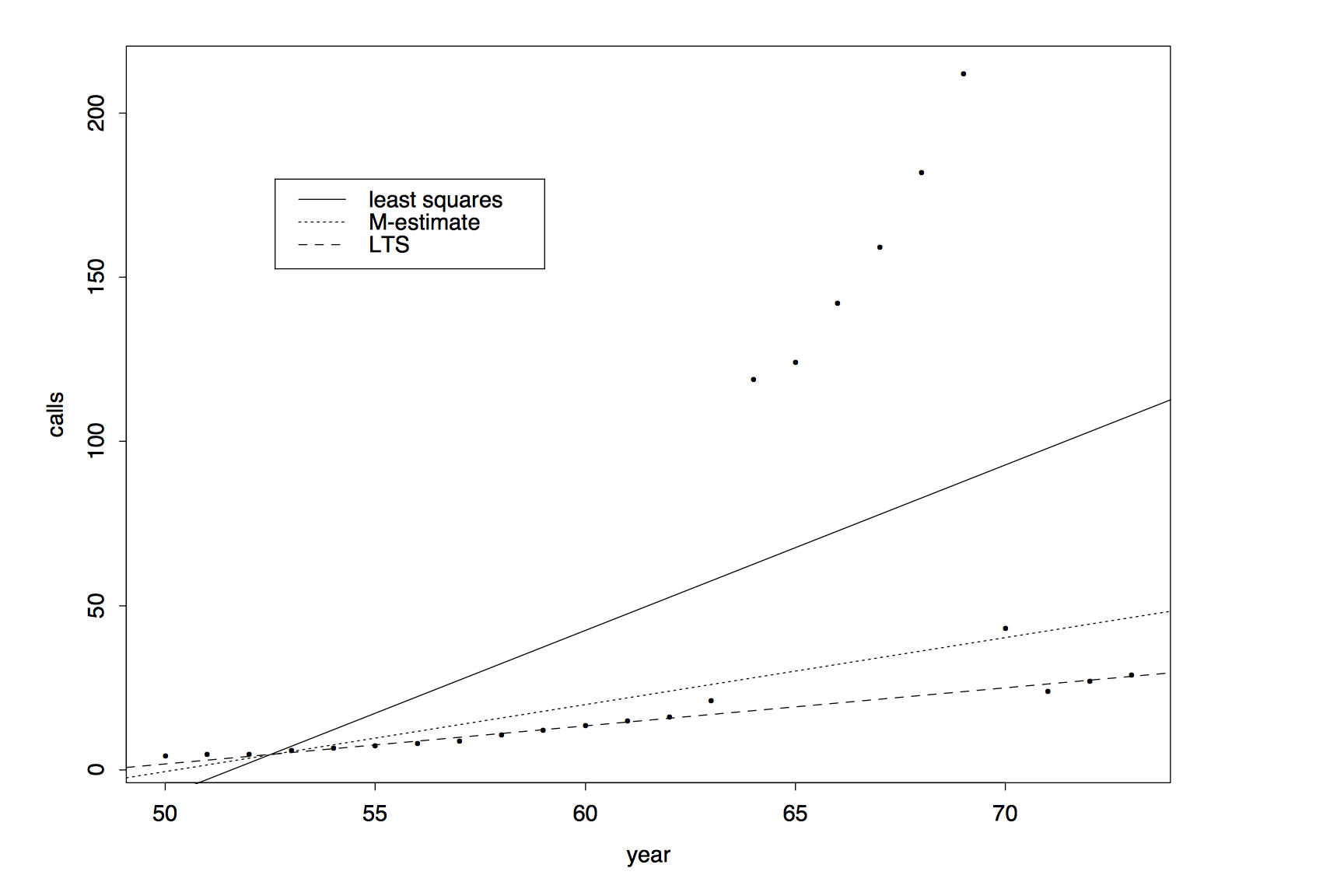 
图中展示出原始数据集中具有大量的离群点，M估计和LTS估计都能够较好的减弱这些离群点对整个回归结果的影响.
本文主要探讨了当普通线性回归模型的假设不成立时的解决方法，特别是在残差不符合正态性假设，残差具有后尾分布的性质，以及数据中出现离群点（强影响点）时对普通模型如何改进能够得到更加稳健的结果. 主要介绍了M估计，最小中值平方法和秩统计量等估计量的方法和性质，并通过一些实例对稳健回归的方法进行了具体的说明. 本章介绍的方法的共同思路是：通过调整各个样本的权重，将强影响点的权重适当调低来达到稳健回归的效果.但是我们要注意到，稳健回归目前并没有得到广泛的应用，例如在使用M估计时，至少有三个方面的问题需要解决：
- 在利用M估计时，如何选择\(\rho(u)\)，特别是当我们不知道残差真实的分布形式时. 目前我们采用的方法都是经验的，先验的；
- 在部分M估计量的\(\rho(u)\)中含有超参数，我们如何确定超参数的值？
- 如何更好地估计M估计量中的\(s\)参数？
这些问题都还有待于在实际运用中加以解决，才能让稳健回归得到较好的效果.另一方面，我们也在实际运用的例子中看到，往往进行稳健回归后所得的拟合直线和普通最小二乘的结果相差并不多，是否值得进行统计上的这样的处理呢？最后像LMS这样的方法，可能在实际计算求解中又遇到新的问题.这些问题都影响了这个方法的普及度.