我们继续介绍流形学习相关的内容. 在这篇文章里我们首先讲一个非常经典的算法，MDS(Multidimensional Scaling), 即所谓的多维尺度分析. 接下来我们再对流形学习里非常经典的Isomap做一个介绍. 事实上Isomap是Tenenbaum在MDS的理论框架上进行一定的改进得到的算法. 这篇文章我们主要参考的是《多元统计分析》课程的讲义和Tenenbaum的Isomap原论文.
MDS
问题
这部分内容可以参考Johnson & Wichern 12.6, Everitt 5.2. 首先我们来看看MDS 想要解决什么样的问题. 我们知道在PCA中，给定样本矩阵\(X(n\times p)\), 可以寻找到一个列数较低的矩阵\(Y(n\times k)\)来表示原来样本中的主要信息. 现在我们来考虑它的反问题，如果我们没有能直接观测到\(X\), 而只是给了一个表达相似程度矩阵(proximity matrix)\(D\)，我们能不能找到样本矩阵\(X\)或者\(Y\)呢？
显然这里的proximity matrix有多种选择，例如相似度，距离，不相似度等等. 值的注意的是，我们对原始数据进行平移、旋转、反射等变换都不应当改变相似度的结果，因此这个问题的解不是唯一的.我们只是想要用一个经典的几何模型或者映射来反应数据之间的相似程度,从而在一定程度上能够有助于我们了解数据的内部结构. 我们可以以欧式距离矩阵为例给出一个算法.
求解
对于样本矩阵\(X(n\times p)\)，欧式距离矩阵\((d_{ij})_{n\times n}\),其中 \[d_{ij}=\sqrt{\sum_{k=1}^p(x_{ik}-x_{jk})^2}=\sum_{k=1}^px_{ik}^2+\sum_{k=1}^px_{jk}^2-2\sum_{k=1}^px_{ik}x_{jk}\] 另一方面，我们考虑\(B=XX'=(XM)(XM)'\)其中\(M\)是正交矩阵.又有 \[b_{ij}=\sum_{k=1}^px_{ik}x_{jk},d_{ij}^2=b_{ii}+b_{jj}-2b_{ij}\] 由此我们可以得到一个解决问题的思路：
- 第一步，我们从欧式距离矩阵\(D\)中想办法找到\(B\)，
- 第二步，再通过\(B\)计算\(V\Lambda V'\)
第一步中，我们知道解不唯一，我们增加这样一个约束：\(\sum_{i=1}^nx_{ik}=0\),从而矩阵\(B\)满足\(\sum_{j=1}^nb_{ij}=\sum_{j=1}^n\sum_{k=1}^px_{ik}x_{jk}=\sum_{k=1}^px_{ik}(\sum_{j=1}^nx_{jk})=0\)即行和为零 在这两个约束下，我们有 \[\sum_{i=1}^nd_{ij}^2=T+nb_{jj},\sum_{j=1}^n\sum_{i=1}^nd_{ij}^2=2nT\] 从而 \[b_{ij}=-\frac{1}{2}[d_{ij}^2-d_{i,}^2-d_{,j}^2+d_{,}^2]\] 其中 \[d_{i,}^2=\frac{\sum_{i=1}^nd_{ij}^2}{n},d_{,j}^2=\frac{\sum_{i=1}^nd_{ij}^2}{n},d_{,}^2=\frac{\sum_{i=1}^n\sum_{j=1}^nd_{ij}^2}{n^2}\] 这样我们就找到了我们的\(b_{ij}\)
第二部我们对\(B\)进行谱分解，得到了\(B=V\Lambda V'\)，其中\(\Lambda\)是对角阵，从而\(V\Lambda^{1/2}\)就是我们所要的\(X\)的一个解.
ISOMAP
通过前面对MDS比较详细的介绍，我们大致了解到，MDS是一种通过数据点之间的相似性的某种度量，来反过来探寻数据之间的相对关系的方法. 而ISOMAP将这种思想进行了一个自然的推广. 正如前面我们对Laplacian Eigenmap算法进行的介绍，我们经常假设高维数据出现在一个低维的流形上，那么此时，通过数据之间的相似性度量（例如测地距离）我们能不能了解到数据的一些情况呢？Isomap正是通过这一思想产生的算法.
算法步骤
- 建立数据的邻接图表示（参见之前介绍Laplacian Eigenmap的另一篇博客.）
- 计算两点之间的最短距离. 这一步实际上是想用Dijkstra算法一类的图上最短路算法来近似流形上两点之间的测地距离. 如果你不知道什么叫测地线或者测地距离的话，你就把它理解成为流形上局部最短的一点曲线.比方说，我们知道在欧氏空间中直线是最短的.但是对于分布在球面上的两点，三维空间中的直线显然不在球面上，球面上连接两点的最短路径是连接这两点的通过球心的圆的一段弧（或者更专业地说，球面上的测地线是大圆的一部分）.这也是为什么从北京飞到西雅图的航班是先往北飞到白令海峡再南下的.
- 将得到的点与点之间的距离矩阵输入MDS算法，得到数据在较低维度下的表示.
从以上步骤中我们可以看出来，Isomap算法是对MDS一个自然的推广.
应用
写到这里，我们似乎没有回答MDS和ISOMAP究竟在解决什么问题，下面我们来看两个例子
MDS与机场相对位置关系
首先，我们来看MDS对这样一个问题的解决:如果我们知道美国若干机场的位置，可以在地图上量出它们的距离. 但是如果我们只有它们之间相互的距离，我们能不能翻过来推出它们之间的相对位置关系呢？ 这个例子来自http://www.benfrederickson.com/multidimensional-scaling/ 假设我们有美国若干机场相互之间的距离，那么我们可以利用R语言的多维尺度分析的方法作出图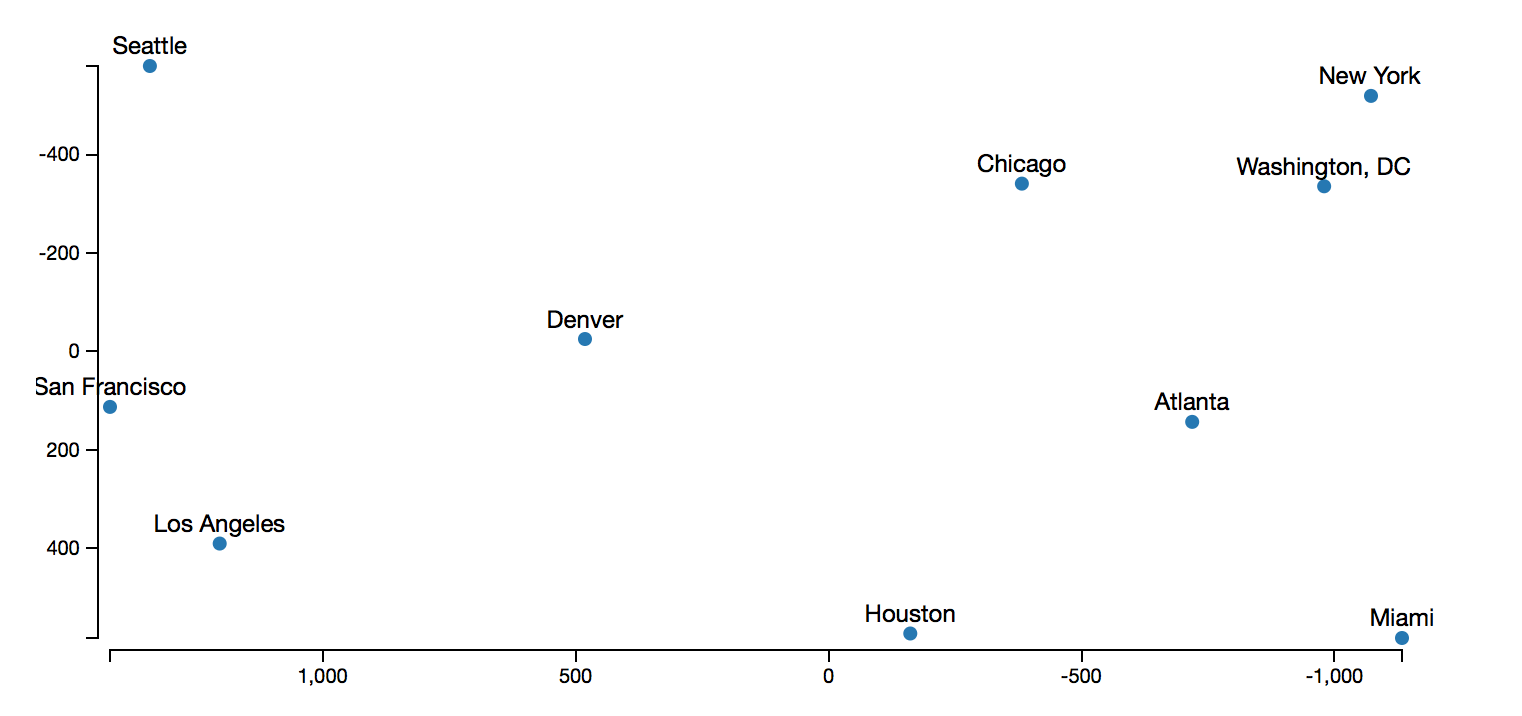 
该图显示了各个机场之前相对的位置关系，有趣的是这张图给出的结果和各个城市在美国地图上的分布大体上也是差不多的.
Isomap 与 瑞士卷数据
瑞士卷数据集是流形学习中一个常用的验证算法效果的数据集.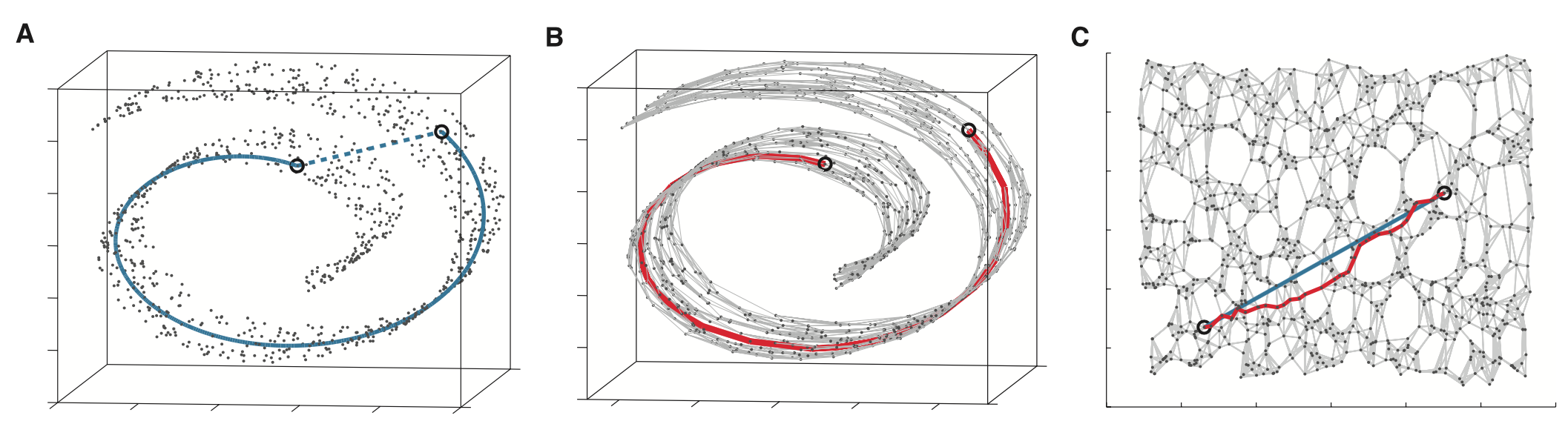 
本图中，A中的蓝色线表示了在流形上两点之间的实际距离，B中的红色是Dijkstra算法在图上找到的最短距离,C表示了这个三维数据集在二维的空间中的嵌入效果. 可以看到Isomap在数据的低维嵌入表示中有着良好的效果.