神经网络作为一个极其热门的领域,在最近几年内席卷了各大研究领域.而有关的内容也是我一直想要学习的.这篇文章是上学期数据挖掘课程的笔记,主要参考了老师的讲义.介绍的内容是神经网络的一些基础概念,从感知器的概念开始,到经典的反向传播算法.作为神经网络这一大类的第一篇文章,我们将重点放在理解原理上,希望能够清楚地解释神经网络的工作方式和训练神经网络的基本过程.
感知器
在深入了解神经网络之前,我们需要回顾感知器的概念.首先,我们研究线性感知器,它是单个神经元的数学模型.我们定义几个概念:
- 输入:\(x_1, \cdots, x_p\)表示来自其他神经元的信号
- 权重:\(w_1, \cdots, w_p\)是树枝状的权重
- 可选常数项\(x_0 = 1\),权重为\(w_0\)
- 激活函数:暂时将我们设置为线性:\[a = \sum_ {i = 0} ^ pw_ix_i \]
下图显示了线性感知器的工作原理. 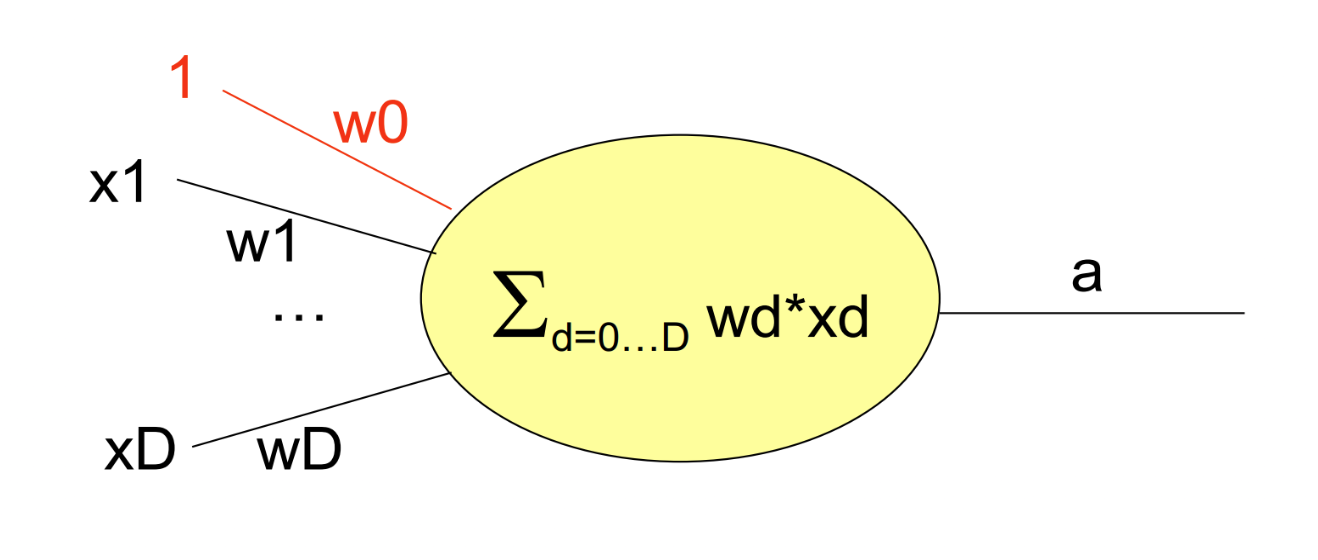
更正式地,在线性感知器中学习使用称为梯度下降的方法:\[w \leftarrow w -\alpha \nabla L(w)\],其中\(\alpha\)是一个称为“学习率”的较小的常数.而\(L\)通常是一个损失函数.例如,对于回归问题,可以将其设置为平方误差损失.然后对于一个样本点\((x,y)\),令\[w\leftarrow w - \alpha(w'x-y)x\]不过我们需要一个停止迭代的标准.
然而,线性感知器可能受到严重的限制.它只是一个线性函数,并不适合二分类问题.这就是为什么我们要演变成非线性感知器. 我们只需更改激活函数\[a = g(w_0x_0 + w_1x_1 + \cdots + w_px_p)\]其中\(g\)是非线性的. 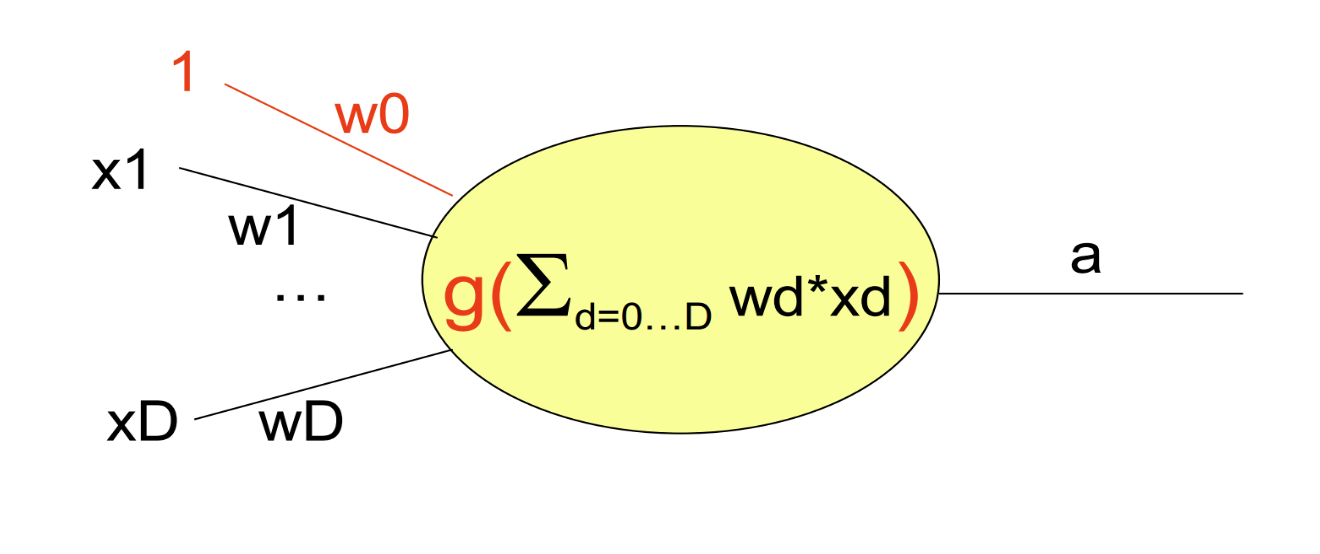
利用单个感知器,我们能表达逻辑上的或OR,与AND,非NOT概念. 下图展示了如何用阶梯函数来进行表示. 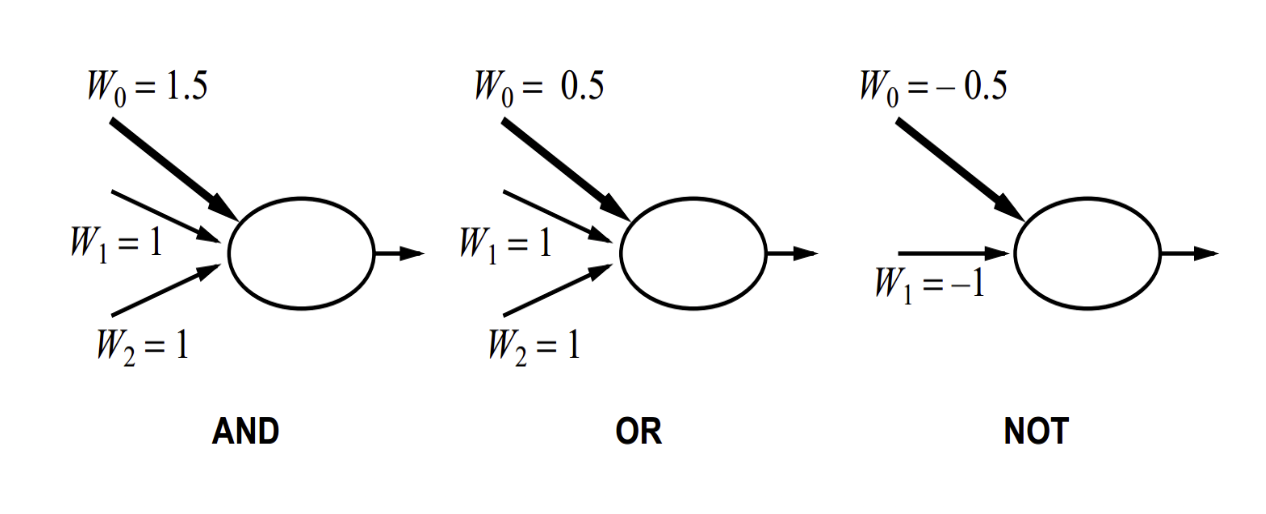
激活函数\(g\)的例子可以是
- LTU:\[g(x)= \begin{cases} 1,\quad x \geq 0 \\0,\quad x <0 \end{cases} \]. LTU感知器不能使用梯度下降来优化.
- sigmoid函数:\[g(x)= \frac{e^x}{1 + e^x} \]
- Rectifier函数:\[g(x)= x^+ = \max(0,x)\]
- tanh函数:\[g(x)= \frac{e^x-e^{-x}} {e^x + e^{ - x}} \]
学习过程非常相似.我们仍然采用梯度下降.例如,对于Sigmoid函数情况,我们有\[g'(x)= g(x)(1-g(x))\] 则具有平方误差损失的梯度下降应为\[w \leftarrow w - \alpha(g-y)g(1-g)x\]
到目前为止,我们仍然使用一个单一的感知器,但是在1969年,一本名为《感知器》(由Marvin Minsky和Seymour Papert所著)的著名的书表明,一个感知器不能学习异或函数XOR.
多层感知器
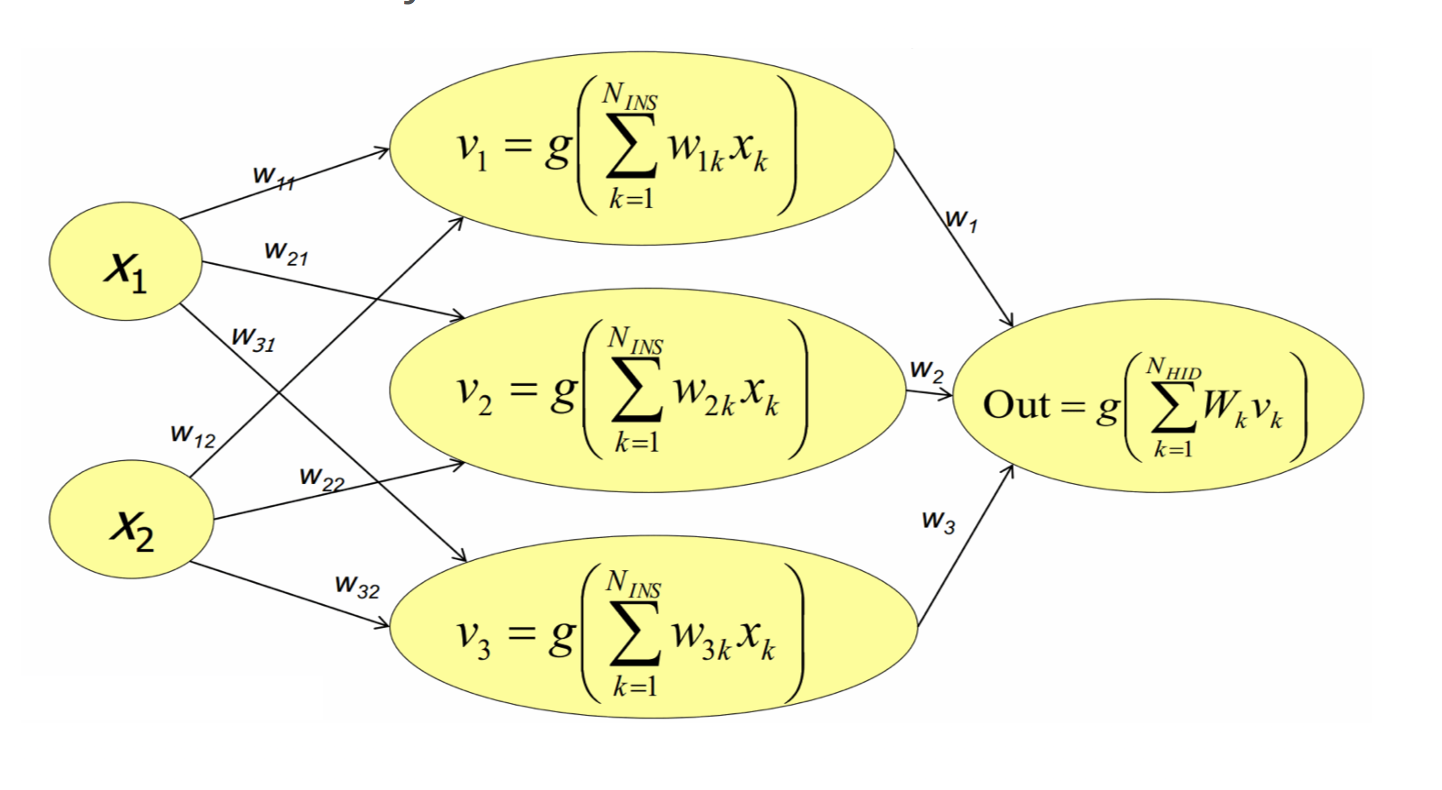
我们可以看到,多层感知器可以比单个感知器更具表现力.我们结合两个相对的sigmoid函数来制作一个脊,然后两个垂直的脊形成一个凸起. 因此,我们可以用不同尺寸大小的凸起来拟合任何表面.
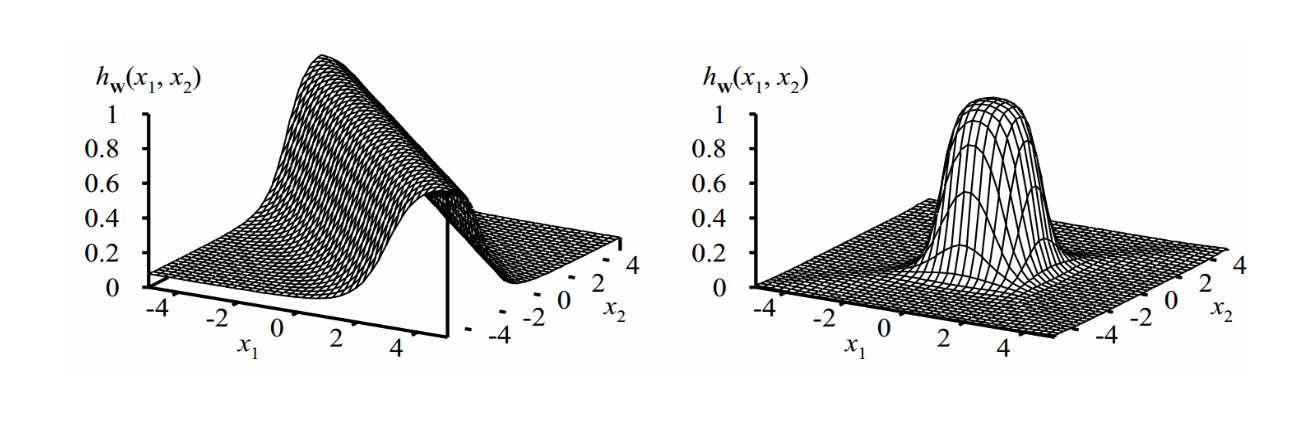
从理论上说,我们不需要太多的层:一个隐藏层网络如果具有足够的隐藏单位神经元,就可以任意准确地表示输入的任何连续函数;两层隐藏网络甚至可以代表不连续函数.
那么我们如何训练MLP?一个着名的算法是反向传播(Back-Propagation).
令 \(x^{(0)}\) 为输入向量,\(u^{(m + 1)} = W^{(m)}x^{(m)}+b^{(m)}\)并且\(x^{(m + 1)} = g(u ^ {(m + 1)})\)是层\(m + 1,m = 0,\cdots,M-1\)的值,其中\(g\)是激活函数.我们以sigmoid函数为例.
回想一下,使用sigmoid函数,梯度将变为\[g'(x)= g(x)(1-g(x))\]层\(x^{(M)}\)是输出.我们还要选择基于\(x^{(M)}\)的损失函数,例如平方误差或交叉熵的总和\(-\sum_{k=1}^Ky_k\log x_k^{(M)}\)
BP算法的几个基本点是
- 初始化系数\(W^{(m)}\)和\(b^{(m)},m=0,1,\cdots,M-1\)到一些小的随机数
- 使用随机梯度下降来更新权重系数.
- 对于训练输入\(x^{(0)}\),计算\(u^{(m)}\)和\(x^{(m)},m = 1,\cdots,M\)
- 计算\(\frac{\partial L}{\partial x^{(M)}}\).例如,在Sigmoid函数和SSE的情况下,该梯度可以是\(2(g-x^{(M)})g(1-g)\)
对于层\(m\)的系数,我们有 \[\frac{\partial L}{\partial W^{(m)}} = \left( \frac{\partial L}{\partial x^{(m + 1)}} \times \nabla g(u^{(m + 1)})\right) \cdot (x^{(m)})^T \]和\[\frac{\partial L}{\partial b^{(m)}} =\frac{\partial L}{\partial x^{(m + 1)}} \times \nabla g(u^{(m + 1)})\] 其中 \(\times\) 表示逐元的乘积. 此外,我们有\[\frac{\partial L}{\partial x^{(m)}} = \text{colSums}\left(W^{(m)}\times \left(\frac{\partial L}{\partial x^{(m + 1)}} \times \nabla g(u^{(m + 1)})\right)\right)\]
另一个重要的事情是决定何时终止反向传播,以避免过度拟合和提前停止.两个可能的答案是在固定次数的迭代后,当保持设置错误开始上升.当训练误差小于阈值时停止它是不正确的,因为这将导致过度拟合.
BP算法图解
这里想分享知乎上的一个高赞回答@龚禹pangolulu 采用了计算图的方法: 这里举一个三层神经网络的例子,输出采用softmax函数,损失函数采用交叉熵. 训练神经网络采用梯度下降的方法,计算函数对参数的导数。 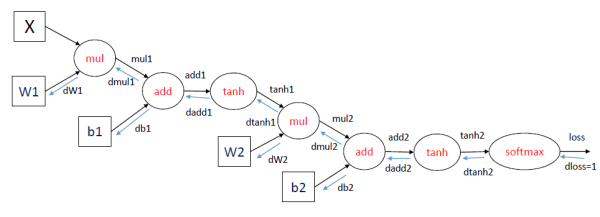
在每一轮迭代中,首先进行forward propagation,也就是计算computation graph中每个节点的状态:
mul1 = X * W1
add1 = mul1 + b1
tanh1 = tanh(add1)
mul2 = tanh1 * W2
add2 = mul2 + b2
tanh2 = tanh(add2)
loss = softmax_loss(tanh2)
之后进行back propagation,也就是计算computation graph中每个节点相对于损失函数(这里表示为loss)的导数,这里面应用了链式法则。对于dloss/dtanh2, dloss/dadd2等导数,下面省略分子直接表示为dtanh2等。
dloss = 1
dtanh2 = softmax_loss_diff(tanh2) * dloss
dadd2 = tanh_diff(add2) * dtanh2
db2 = 1 * dadd2
dmul2 = 1 * dadd2
dW2 = tanh1 * dmul2
dtanh1 = W2 * dmul2
dadd1 = tanh_diff(add1) * dtanh1
db1 = 1 * dadd1
dmul1 = 1 * dadd1
dW1 = X * dmul1
其中dW1,dW2,db1和db2就是我们需要求的参数的梯度.
最后, 关于神经网络的调参,要考虑的问题非常多. 例如,网络结构,学习率选取等等都可能会对训练结果造成影响. 在机器学习算法中通用的cross-validation调参是一种常见的方法,而更多的调参技巧将在之后的文章中介绍。